Preis-Absatz-Funktion
In der Theorie kann der Absatz durch den Preis beeinflusst werden. In der Praxis gibt es allerdings viele andere Einflussgrößen, die es zu beachten gilt, wie die im nächsten Beitrag deklarierte „Empirische Preis-Absatz-Funktion“ (Empirische Preis-Absatz-Funktion (brain365.de)).
Klassische Preistheorie
Individuelle Preis-Absatz-Funktionen (PAFs)
- beschreiben in der Theorie den Zusammenhang zwischen Preis und Absatz
- besagen, dass der Preis den Absatz beeinflusst (d.h. durch Preisänderung lässt sich der Absatz ändern).
Es gibt zwei Fälle:
- Ja / Nein – Fall
wenn der Preis zu hoch ist, findet KEIN Absatz statt
z.B. bei Investitionsgütern, d.h. bei hochpreisigen Gütern - Variable Menge – Fall
– je höher der Preis, desto geringer ist die Absatzmenge
– je geringer der Preis, desto höher ist die Absatzmenge
z.B. bei Verbrauchs-, oder Gebrauchsgütern
Maximalpreis ist bei der klassischen Preis-Absatz-Funktion der Preis, bei welchen die Absatzmenge = 0 wäre, weil kein Kunde mehr das Produkt kaufen würde.
Aggregation individueller Preis-Absatz-Funktionen
wird angewendet, wenn die Funktion für mehr als einen Kunden / Konsumenten ausgeführt wird, wobei die Summen-Funktion ausgeführt wird, d.h. die Einzelwerte der preisabhängigen Absatzmengen werden addiert und die Summe wird graphisch dargestellt..
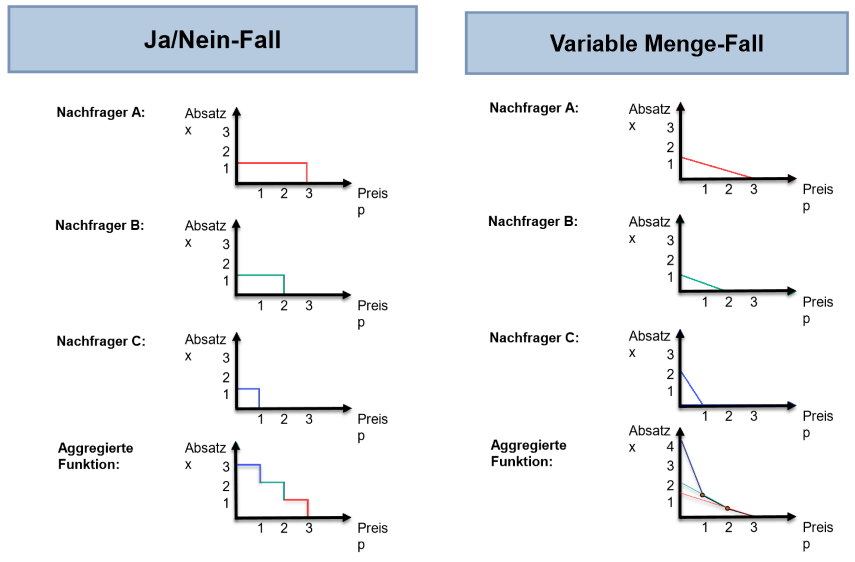
Ja / Nein – Fall Beispiel:
- Nachfrager A, B und C haben einen unterschiedliche Preisbereitschaften
A ist bereit für 1 Mengeneinheit des Produktes maximal 3 Preiseinheiten zu bezahlen
B ist bereit für 1 Mengeneinheit des Produktes maximal 2 Preiseinheiten zu bezahlen
C ist bereit für 1 Mengeneinheit des Produktes maximal 1 Preiseinheit zu bezahlen
In Summe haben die drei Nachfrager eine Zahlungsbereitschaft die von 1 Preiseinheit über 2 bis zu 3 Preiseinheiten geht, die für drei unterschiedliche Einheiten maximal bezahlt werden
Variable Menge-Fall Beispiel:
- Nachfrager A, B und C haben einen unterschiedliche Preisbereitschaften
A beschafft sich 1,5 Mengeneinheiten, wenn er 0 Preiseinheiten bezahlen muss, kauft 1 Mengeneinheit, wenn er 1 Preiseinheit bezahlen muss und 0,5 Mengeneinheiten, wenn er 2 Preiseinhalten zahlen muss und 0 Mengeneinheiten, wenn er 3 Preiseinheiten zahlen muss
B beschafft sich 1 Mengeneinheiten, wenn er 0 Preiseinheiten bezahlen muss, kauft 0,5 Mengeneinheit, wenn er 1 Preiseinheiten bezahlen muss und 0 Mengeneinheiten, wenn er 1,5 Preiseinheit bezahlen muss.
C beschafft sich 2 Mengeneinheiten, wenn er 0 Preiseinheiten bezahlen muss, 1 Mengeneinheit, wenn er 0,5 Preiseinheiten bezahlten muss und 0 Mengeneinheiten, wenn er 1 Preiseinheit bezahlen muss.
In Summe hat die Gruppe der Nachfrager folgende Zahlungsbereitschaft:- die Gruppe beschafft maximal 4 Mengeneinheiten, bei einem Preis von 0 Einheiten
- sie kauft 1,5 Mengeneinheiten, bei 1 Preiseinheit
- sie kauft 0,5 Mengeneinheiten, bei 2 Preiseinheiten
- sie kauft 0 Mengeneinheiten, bei 3 Preiseinheiten
In der Literatur gibt es mathematische Formeln zur Preis-Absatz-Funktion und zur Preiselastizität.
Es gibt die lineare und die multiplikative Preis-Absatzfunktion.
Lineare Preis-Absatzfunktion
Die lineare Preis-Absatz-Funktion geht davon aus, dass die Änderung des Preises um jeweils 1 Preiseinheit immer zur, in Relation zum Absatz, gleichen Änderung des Absatzes führt, also sich Preis und Absatz linear zueinander verändern, unabhängig davon, welches Preisniveau (hoch oder niedrig) der Preis, repräsentiert durch einen Preispunkt in der Grafik, hat.

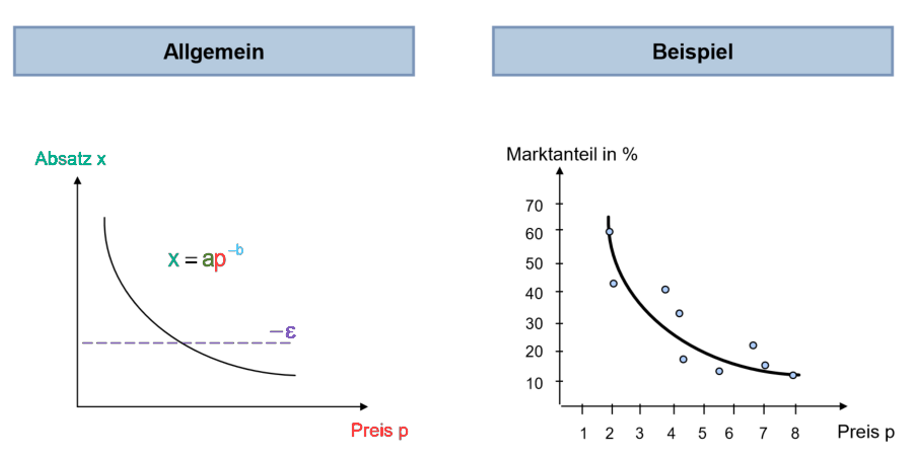
Multiplikative Preis-Absatzfunktion
Bei der multiplikativen Preis-Absatz-Funktion ist die absolute Wirkung einer Preisänderung abhängig vom Preisniveau. Es geht also bei der multiplikativen PAF darum, aufgrund einer relativen Preisänderung, die sich auf den Absatz auswirkt, eine relative Absatzänderung zu berechnen. Diese Absatzänderung geht von der zuletzt berechneten bzw. der ausgehenden Basis (letzter Preispunkt) aus. b ist somit ein Faktor, der die relative Absatzänderung ausdrückt, d.h. ein negativer Exponent (siehe Formeln oben), so dass
- Bei der Änderung eines sehr geringen Preises um den Wert x (z.B. von 2 auf 1) wird eine sehr hohe absolute Änderung des Absatzes erzeugt. (Halbierung des Preises)
- Bei der Änderung eines sehr hohen Preises um den gleichen Wert x (z.B. von 20 auf 19) wird ein sehr geringe absolute Änderung des Absatzes erzeugt.
- Absolut betrachtet ist die Preisänderung gleich – nämlich EINE Preiseinheit.
- aber die Änderung bei einer kleineren Basis ist relativ gesehen eine Halbierung (von 2 auf 1 = Halbierung)
Dies hat auch mit der Preispsychologie zu tun:
Kunden schauen sich die relativen Preisunterschiede an und nicht die absoluten Preisänderungen.
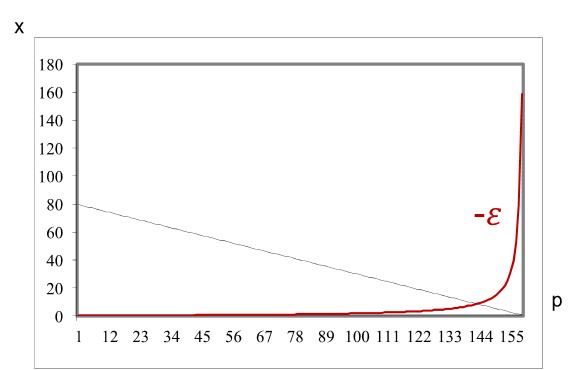
Preiselastizität
Die Preiselastizität E ist ein Maß für die Stärke der Wirkung des Preises auf den Absatz x. Sie gibt das Verhältnis der relativen Änderung des Absatzes zu der sie verursachenden relativen Änderung des Preises an.
- Relative Größen werden benötigt für den Vergleich von PAF über mehrere Produkte (z.B. eines Produktprogramms) hinweg, die ggf. unterschiedliche Mengeneinheiten (kg, Stück..etc.) haben.
- Bei der linearen Preis-Absatz-Funktion hat die Elastizität an jeder Stelle einen anderen Wert, weil die absolute Absatzänderung konstant bleibt, jedoch der jeweilige Basis-Ausgangswert / Preispunkt sich hierfür mit jeder Preis/Absatz-Änderung ändert.
Da es sich hierbei vor allem um theoretische Ansätze handelt (die den grundsätzlichen Zusammenhang dokumentieren) gehen wir nicht näher auf die Formeln, Regeln und Berechnungen ein.
