Produktionsprogrammplanung in der Serien- oder Sortenfertigung bei mehreren möglichen Engpässen

Besteht bei einem Unternehmen, das Serien oder Sorten von Erzeugnissen mehrstufig produziert mehr als ein möglicher Engpass so kann die Effektivität der Produktionsprogrammplanung über die sogenannte lineare Programmierung (LP) durchgeführt werden.

Was bedeutet – “mehr als einen möglichen Engpass”:
Wenn es n Produkte A, B, C.. gibt
und es m Maschinen 1, 2 3 .. gibt
und viele Produkte durch mehrere Maschinen gefertigt werden in jeweils x Stufen (je x Arbeitsgänge), aber Produkt A belastet Maschine 1 kapazitiv “sehr stark” und nicht Maschine 2 (d.h. der Arbeitsgang auf Maschine 1 läuft länger als der auf Maschine 2 beim Produkt A)
und Produkt B belastet Maschine 2 kapazitiv “sehr stark” und nicht Maschine 1 (d.h. der Arbeitsgang auf Maschine 2 läuft länger als der auf Maschine 1 beim Produkt B) etc.
dann ist eine Produktionsprogrammplanung nötig, die mehrere mögliche Engpässe berücksichtigt.

Welche Maschine wird zum Engpass?
– wenn sehr viel von Produkt A gefertigt wird, dann wird Maschine 1 zum Engpass
– wenn sehr viel von Produkt B gefertigt wird, dann wird Maschine 2 zum Engpass
…usw.
Es ist auch möglich, dass beide Maschinen zur Engpass-Ressource werden.

Welche Maschine zum Engpass wird, hängt vom Produktionsprogramm ab, d.h. davon von welchem Produkt welche Menge gefertigt werden soll. Es wird somit von “programmabhängigen Engpässen” gesprochen, weil der Engpass nicht eindeutig feststeht, sondern von unterschiedlichen Bedingungen abhängt.

Durch die lineare Programmierung (Optimierung durch Aufbau eines LP-Modells) kann unter Annahme sich ändernder Bedingungen und Einflussgrößen ermittelt werden, unter welchen Umständen keine, eine oder mehrere Maschinen zum Engpass werden.

Bei der linearen Programmierung zur Produktionsprogrammplanung mit mehreren möglichen Engpässen wird auch von dem Aufbau eines LP-Modells (ist ein mathematisches Planungsmodell) gesprochen.

Dieses LP-Modell

• kann eine Zielfunktion haben, das LINEAR ist
  1. entweder eine Kostenfunktion zur Minimierung der Kosten
  2. oder eine Gewinnfunktion zur Maximierung des Gewinns
      
• berücksichtigt ein System von Nebenbedingungen, die auch jeweils LINEAR sind
  1. Kapazitätsbedingungen (jede Maschine / Ressource steht nur begrenzt zur Verfügung)
  2. Beschaffungsgrenzen (für jedes Material gibt es maximale Beschaffungsmengen)
  3. Absatzgrenzen (es gibt für jedes Produkt maximale Absatzmengen)

ERP-Systeme, die das Simplex-Verfahren für die lineare Programmierung beherrschen, können die Effektivität in der Produktion mit mehreren möglichen Engpässen unterstützen. Gleiches gilt für Anwendungssysteme, welche die komplexe regelbasierte Anlage von Produktionsplänen beherrschen.

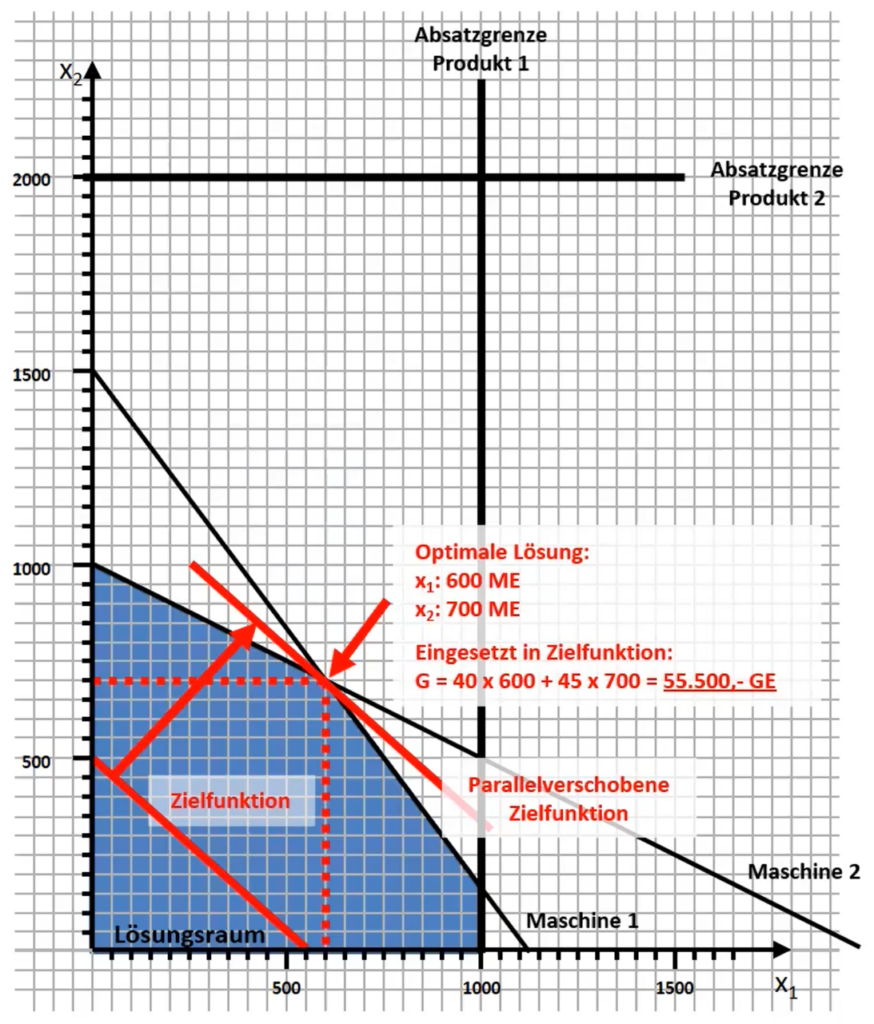
Beispiel eines LP-Modells mit 2 Produkten und 2 Maschinen (vereinfachtes Beispiel zu Illustration):